Two-state quantum system
In quantum mechanics, a two-state system (also known as a TLS or two-level system) is a system which has two possible states. More formally, the Hilbert space of a two-state system has two degrees of freedom, so a complete basis spanning the space must consist of two independent states. An example of a two-state system is the spin of a spin-1/2 particle such as an electron, whose spin can have values +½ or -½ in units of ħ.
The physics of a quantum mechanical two-state system is trivial if both states are degenerate, that is, if the states have the same energy. However, if there is an energy difference between the two states, then nontrivial dynamics can occur.
Contents |
Two-state dynamics
If the time-independent Hamiltonian is 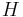 , and we label the two levels as
, and we label the two levels as 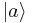 and
and 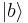 with corresponding orthonormal energy eigenvalues
with corresponding orthonormal energy eigenvalues 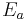 and
and 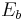 , then the dynamics of the system can be specified as follows:
, then the dynamics of the system can be specified as follows:
At some time 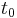 , let the system be in an arbitrary (and completely general) state,
, let the system be in an arbitrary (and completely general) state, 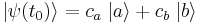 then after evolving under
then after evolving under 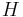 , at time
, at time 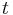 , the state will be
, the state will be
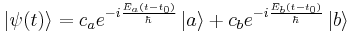
The physics of two state systems can be usefully applied to multi-state systems where the system is known to have only enough energy available to excite the lowest two states, thus effectively creating a two state system. In fact, in nature, it is difficult to identify any true two-state systems; merely systems where the energetics of the circumstances isolate two particular states.
The set of all states in a two-level system can be mapped onto a representation known as the Bloch sphere.
Dynamics of a two state system interacting with a field
Free Precession
The interaction of a two state system with an external field results in the precession of the state vector. The ability to carefully control the position of the state vector on the Bloch sphere is central to the realization of the qubit. Consider the case of a spin-1/2 particle in a magnetic field. The interaction Hamiltonian for this system is
where  is the magnitude of the particle's magnetic moment,
is the magnitude of the particle's magnetic moment, 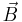 is the magnetic field, and
is the magnetic field, and 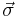 is the vector of Pauli matrices. In analogy to related systems,
is the vector of Pauli matrices. In analogy to related systems,  is a coupling constant, and
is a coupling constant, and 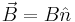 is an external field. Solving the time dependent Schrödinger equation
is an external field. Solving the time dependent Schrödinger equation 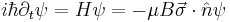 yields the solution
yields the solution
where 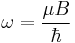 ,
, 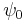 is the state vector at time
is the state vector at time 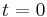 , and
, and 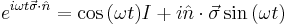 . Physically, this corresponds to the Bloch vector precessing around
. Physically, this corresponds to the Bloch vector precessing around 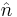 with angular frequency
with angular frequency 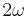 . Without loss of generality, assume the field points in
. Without loss of generality, assume the field points in 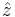 , such that
, such that
The representation on the Bloch sphere for a state vector 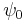 will simply be the vector of expectation values
will simply be the vector of expectation values 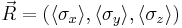 . As an example, consider a state vector
. As an example, consider a state vector 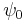 that is a normalized superposition of
that is a normalized superposition of 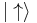 and
and 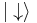 , that is, a vector that can be represented in the
, that is, a vector that can be represented in the 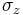 basis as
basis as
its components on the Bloch sphere will simply be 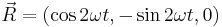 . This is a unit vector that begins pointing in
. This is a unit vector that begins pointing in 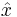 and precesses around
and precesses around 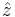 in a left-handed manner. In general, by a rotation around
in a left-handed manner. In general, by a rotation around 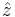 , any state vector
, any state vector 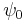 can be represented as
can be represented as 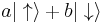 with real coefficients
with real coefficients  and
and  . Such a state vector corresponds to a Bloch vector in the
. Such a state vector corresponds to a Bloch vector in the 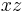 plane making an angle
plane making an angle  with the
with the  -axis. This vector will proceed to precess around
-axis. This vector will proceed to precess around 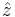 . In theory, by allowing the system to interact with the field of a particular direction and strength for precise durations, it is possible to obtain any orientation of the Bloch vector, which is equivalent to obtaining any complex superposition. This is the basis for numerous technologies including quantum computing and MRI.
. In theory, by allowing the system to interact with the field of a particular direction and strength for precise durations, it is possible to obtain any orientation of the Bloch vector, which is equivalent to obtaining any complex superposition. This is the basis for numerous technologies including quantum computing and MRI.
NMR
NMR is an important example in the dynamics of two-state systems because it is involves the exact solution to a time dependent Hamiltonian. Consider a spin-1/2 particle in a magnetic field
This corresponds physically to a situation where there is a time independent field of strength 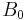 pointing in
pointing in 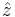 , and a field of strength
, and a field of strength 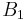 rotating in a right-handed manner with an angular frequency
rotating in a right-handed manner with an angular frequency 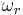 . The dynamics of this situation are found as above by solving the time dependent Schrödinger equation
. The dynamics of this situation are found as above by solving the time dependent Schrödinger equation
Which, after dividing through by 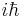 and expanding out the dot product is
and expanding out the dot product is
where 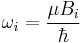 . To remove the time dependence from the problem, the wave function is transformed according to
. To remove the time dependence from the problem, the wave function is transformed according to 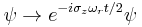 . The time dependent Schrödinger equation becomes
. The time dependent Schrödinger equation becomes
Which after some rearrangement yields
Evaluating each term on the right hand side of the equation
The equation now reads
Which by Euler's identity becomes
As per the previous section, the solution to this equation has the Bloch vector precessing around 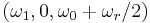 with a frequency that is twice the magnitude of the vector. If
with a frequency that is twice the magnitude of the vector. If 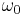 is sufficiently strong, some proportion of the spins will be pointing directly down prior to the introduction of the rotating field. If the angular frequency of the rotating magnetic field is chosen such that
is sufficiently strong, some proportion of the spins will be pointing directly down prior to the introduction of the rotating field. If the angular frequency of the rotating magnetic field is chosen such that 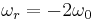 , in the rotating frame the state vector will precess around
, in the rotating frame the state vector will precess around 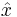 with frequency
with frequency 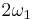 , and will thus flip from down to up releasing energy in the form of detectable photons. This is the fundamental basis for NMR, and in practice is accomplished by scanning
, and will thus flip from down to up releasing energy in the form of detectable photons. This is the fundamental basis for NMR, and in practice is accomplished by scanning 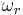 until the resonant frequency is found at which point the sample will emit light. Similar calculations are done in atomic physics, and in the case that the field is not rotating, but oscillating with a complex amplitude, use is made of the rotating wave approximation in deriving such results.
until the resonant frequency is found at which point the sample will emit light. Similar calculations are done in atomic physics, and in the case that the field is not rotating, but oscillating with a complex amplitude, use is made of the rotating wave approximation in deriving such results.
Relation to Bloch equations
The Bloch equations for a collection of spin-1/2 particles can be derived from the time dependent Schrödinger equation for a two level system. Starting with the previously stated Hamiltonian 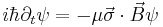 , it can be written in summation notation after some rearrangement as
, it can be written in summation notation after some rearrangement as
Multiplying by a Pauli matrix 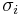 and the conjugate transpose of the wavefunction, and subsequently expanding the product of two Pauli matrices yields
and the conjugate transpose of the wavefunction, and subsequently expanding the product of two Pauli matrices yields
Adding this equation to its own conjugate transpose yields a left hand side of the form
And a right hand side of the form
As previously mentioned, the expectation value of each Pauli matrix is a component of the Bloch vector, 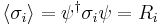 . Equating the left and right hand sides, and noting that
. Equating the left and right hand sides, and noting that 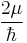 is the gyromagnetic ratio
is the gyromagnetic ratio  , yields another form for the equations of motion of the Bloch vector
, yields another form for the equations of motion of the Bloch vector
where the fact that 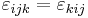 has been used. In vector form these three equations can be expressed in terms of a cross product
has been used. In vector form these three equations can be expressed in terms of a cross product
Classically, this equation describes the dynamics of a spin in a magnetic field. An ideal magnet consists of a collection of identical spins behaving independently, and thus the total magnetization 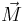 is proportional to the Bloch vector
is proportional to the Bloch vector 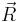 . All that is left to obtain the final form of the Bloch equations is the inclusion of the phenomenological relaxation terms.
. All that is left to obtain the final form of the Bloch equations is the inclusion of the phenomenological relaxation terms.
As a final aside, the above equation can be derived by considering the time evolution of the angular momentum operator in the Heisenberg picture.
Which, when coupled with the fact that 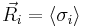 , is the same equation as before.
, is the same equation as before.
Examples of two-state quantum systems
- Spin-1/2 particles are two-state quantum systems when only the spin degree of freedom is considered.
- The "inverting" degree of freedom in an ammonia molecule; the nitrogen at the vertex of an ammonia molecule exhibits two molecular states - "up" and "down", corresponding to opposite positions with respect to the plane of the three hydrogen atoms. In an electric field, these two states are non-degenerate.
- Two-level systems are important in the field of quantum computing as they are used to implement qubits.
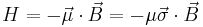
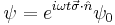
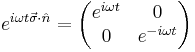
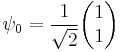
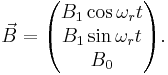
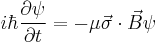
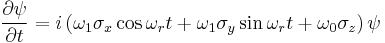
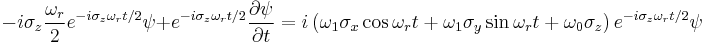
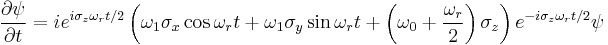
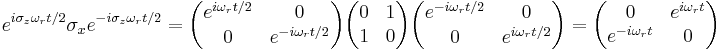
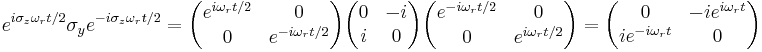
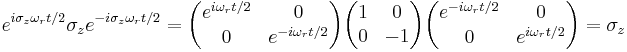
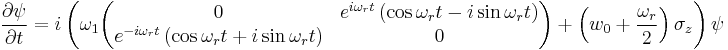
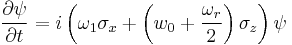
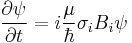
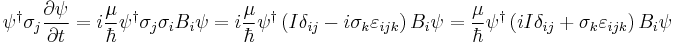
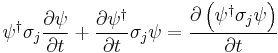
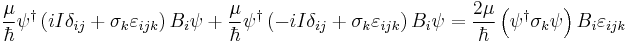
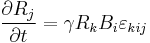
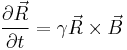
![i\hbar\frac{d\sigma_j}{dt}=[\sigma_j,H]=[\sigma_j, -\mu \sigma_i B_i]=-\mu\left(\sigma_j\sigma_i B_i - \sigma_i\sigma_j B_i\right)=\mu[\sigma_i,\sigma_j]B_i = 2\mu i \varepsilon_{ijk}\sigma_k B_i](/2012-wikipedia_en_all_nopic_01_2012/I/1e943bd74fe3207173e677fe1746effd.png)